Giải Toán 10 trang 16 Tập 2 Kết nối tri thức

Giải Toán 10 trang 16 Tập 2

Bài 6.7 trang 16 Toán 10 Tập 2: Vẽ các đường parabol sau:

a) y = x2 - 3x + 2;

b) y = - 2x2 + 2x + 3;

c) y = x2 + 2x + 1;

d) y = - x2 + x - 1.

Lời giải

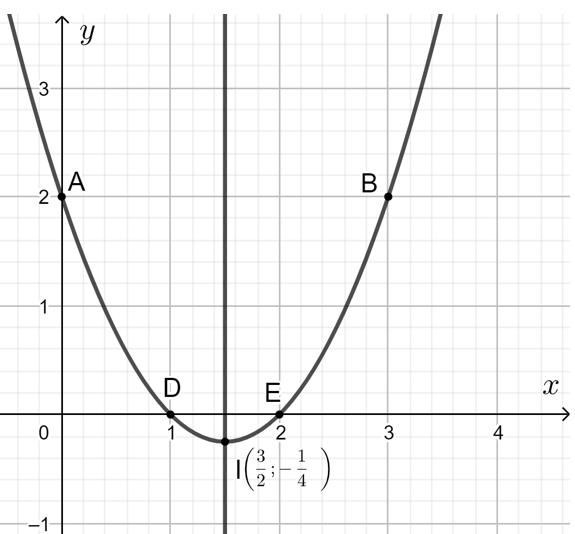
a) y = x2 - 3x + 2

Hệ số a = 1 > 0 nên parabol quay bề lõm lên trên.

Parabol y = x2 - 3x + 2 có:

- Tọa độ đỉnh I32;−14;

- Trục đối xứng x=32;

- Giao điểm của đồ thị với trục Oy là A(0; 2).

- Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình x2 - 3x + 2 = 0, tức là x = 2 và x = 1 hay giao điểm với Ox là D(1; 0) và E(2; 0);

- Điểm đối xứng với điểm A qua trục đối xứng x=32 là B(3; 2).

Vẽ đường cong đi qua các điểm trên ta được parabol y = x2 - 3x + 2.

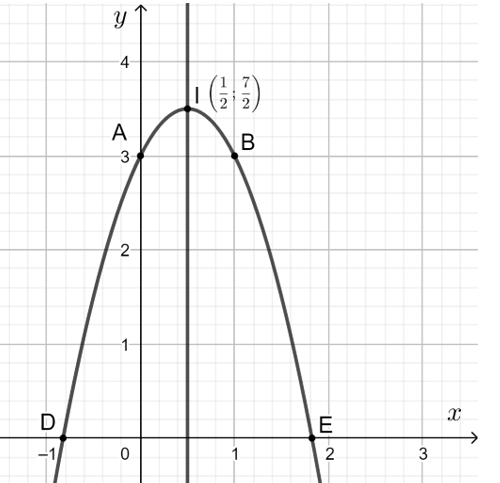
b) y = - 2x2 + 2x + 3

Hệ số a = - 2 < 0 nên parabol quay bề lõm xuống dưới.

Parabol y = - 2x2 + 2x + 3 có:

- Tọa độ đỉnh I12;72;

- Trục đối xứng x=12;

- Giao điểm của đồ thị với trục Oy là A(0; 3).

- Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình - 2x2 + 2x + 3 = 0, tức là x = 1+72 và x = 1−72 hay giao với Ox là D1−72;0 và E1+72;0;

- Điểm đối xứng với điểm A qua trục đối xứng x=12 là B(1; 3).

Vẽ đường cong đi qua các điểm trên ta được parabol y = - 2x2 + 2x + 3.

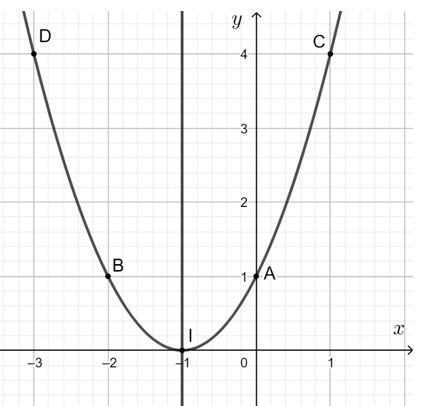
c) y = x2 + 2x + 1

Hệ số a = 1 > 0 nên parabol quay bề lõm lên trên.

Parabol y = x2 + 2x + 1 có:

- Tọa độ đỉnh I(- 1; 0)

- Trục đối xứng x = - 1;

- Giao điểm của đồ thị với trục Oy là A(0; 1).

- Điểm đối xứng với điểm A qua trục đối xứng x = - 1 là B(- 2; 1).

- Lấy điểm C(1; 4) thuộc parabol, điểm đối xứng với C qua trục đối xứng x = - 1 là D(- 3; 4).

Vẽ đường cong đi qua các điểm trên ta được parabol y = x2 + 2x + 1.

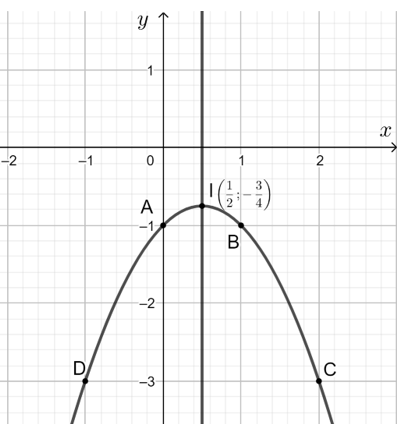
d) y = - x2 + x - 1

Hệ số a = - 1 < 0 nên parabol quay bề lõm xuống dưới.

Parabol y = - x2 + x - 1 có:

- Tọa độ đỉnh I12;−34;

- Trục đối xứng x=12;

- Giao điểm của đồ thị với trục Oy là A(0; - 1).

- Điểm đối xứng với điểm A qua trục đối xứng x=12 là B(1; - 1).

- Lấy điểm C(2; - 3) thuộc parabol, điểm đối xứng với trục đối xứng x=12 là D(- 1; - 3).

Vẽ đường cong đi qua các điểm trên ta được parabol y = - x2 + x - 1.

Bài 6.8 trang 16 Toán 10 Tập 2: Từ các parabol đã vẽ ở Bài tập 6.7, hãy cho biết khoảng đồng biến và khoảng nghịch biến của mỗi hàm số bậc hai tương ứng.

Lời giải

a) Đồ thị hàm số đi xuống từ trái qua phải trên khoảng −∞;32 nên hàm số y = x2 - 3x + 2 nghịch biến trên khoảng −∞;32.

Đồ thị hàm số đi lên từ trái qua phải trên khoảng 32;+∞ nên hàm số y = x2 - 3x + 2 đồng biến trên khoảng 32;+∞.

b) Đồ thị hàm số đi lên từ trái qua phải trên khoảng −∞;12 nên hàm số y = - 2x2 + 2x + 3 đồng biến trên khoảng −∞;12.

Đồ thị hàm số đi xuống từ trái qua phải trên khoảng 12;+∞ nên hàm số y = - 2x2 + 2x + 3 nghịch biến trên khoảng 12;+∞.

c) Đồ thị hàm số đi xuống từ trái qua phải trên khoảng (- ∞; - 1) nên hàm số y = x2 + 2x + 1 nghịch biến trên khoảng (- ∞; - 1).

Đồ thị hàm số đi lên từ trái qua phải trên khoảng (- 1; +∞) nên hàm số y = x2 + 2x + 1 đồng biến trên khoảng (- 1; +∞).

d) Đồ thị hàm số đi lên từ trái qua phải trên khoảng −∞;12 nên hàm số y = - x2 + x - 1 đồng biến trên khoảng −∞;12.

Đồ thị hàm số đi xuống từ trái qua phải trên khoảng 12;+∞ nên hàm số y = - x2 + x - 1 nghịch biến trên khoảng 12;+∞.

Bài 6.9 trang 16 Toán 10 Tập 2: Xác định parabol y = ax2 + bx + 1, trong mỗi trường hợp sau:

a) Đi qua hai điểm A(1; 0) và B(2; 4);

b) Đi qua điểm A(1; 0) và có trục đối xứng x = 1;

c) Có đỉnh I(1; 2);

d) Đi qua điểm C(- 1; 1) và có tung độ đỉnh bằng - 0,25.

Lời giải

Điều kiện: a ≠ 0.

a) Parabol y = ax2 + bx + 1 đi qua điểm A(1; 0) nên thay x = 1, y = 0 vào hàm số y = ax2 + bx + 1 ta có 0 = a . 12 + b . 1 + 1 ⇔ a + b + 1 = 0 ⇔ a = - 1 - b (1).

Parabol y = ax2 + bx + 1 đi qua điểm B(2; 4) nên thay x = 2, y = 4 vào hàm số y = ax2 + bx + 1 ta có 4 = a . 22 + b . 2 + 1 ⇔ 4a + 2b = 3 (2).

Thay (1) vào (2) được: 4 . (- 1 - b) + 2b = 3 ⇔ - 2b = 7 ⇔ b = −72.

Do đó, a = - 1 −−72=52.

Vậy y=52x2−72x+1.

b) Parabol y = ax2 + bx + 1 đi qua điểm A(1; 0) nên thay x = 1, y = 0 vào hàm số y = ax2 + bx + 1 ta có 0 = a . 12 + b . 1 + 1 ⇔ a + b + 1 = 0 ⇔ a = - 1 - b (3).

Parabol y = ax2 + bx + 1 có trục đối xứng x = 1 nên −b2a=1⇔2a=−b (4).

Thay (3) vào (4) được: 2 . (- 1 - b) = - b ⇔ b = - 2.

Do đó, a = - 1 - (- 2) = 1.

Vậy y = x2 - 2x + 1.

c) Parabol y = ax2 + bx + 1 có đỉnh I(1; 2).

Khi đó −b2a=1⇔2a=−b (5).

Và 2 = a . 12 + b . 1 + 1 ⇔ a + b = 1 ⇔ a = 1 - b (6).

Thay (6) vào (5) ta được: 2 . (1 - b) = - b ⇔ b = 2.

Khi đó a = 1 - 2 = - 1.

Vậy y = - x2 + 2x + 1.

d) Parabol y = ax2 + bx + 1 đi qua điểm C(- 1; 1) nên thay x = - 1 và y = 1 vào hàm số y = ax2 + bx + 1 ta có 1 = a . (- 1)2 + b . (- 1) + 1 ⇔ a - b = 0 ⇔ a = b.

Ta có: ∆ = b2 - 4ac = a2 - 4 . a . 1 = a2 - 4a.

Tung độ đỉnh bằng - 0,25 nên −Δ4a=−0,25⇔a2−4a4a=0,25

⇔aa−44a=14⇔a−44=14 (do a ≠ 0)

⇔ a - 4 = 1 ⇔ a = 5.

Vậy a = b = 5.

Vậy y = 5x2 + 5x + 1.

Bài 6.10 trang 16 Toán 10 Tập 2: Xác định parabol y = ax2 + bx + c, biết rằng parabol đó đi qua điểm A(8; 0) và có đỉnh là I(6; - 12).

Gợi ý: Phương trình parabol có thể viết dưới dạng y = a(x - h)2 + k, trong đó I(h; k) là tọa độ đỉnh của parabol.

Lời giải

Điều kiện: a ≠ 0.

Do parabol có đỉnh là I(6; - 12) nên phương trình parabol có dạng y = a(x - 6)2 - 12.

Lại có parabol đi qua điểm A(8; 0) nên thay x = 8 và y = 0 vào hàm số trên ta có:

0 = a(8 - 6)2 - 12 ⇔ a . 4 - 12 = 0 ⇔ a = 3 (thỏa mãn).

Vậy phương trình parabol là y = 3(x - 6)2 - 12 hay y = 3x2 - 36x + 96.

Bài 6.11 trang 16 Toán 10 Tập 2: Gọi (P) là đồ thị hàm số bậc hai y = ax2 + bx + c. Hãy xác định dấu của hệ số a và biệt thức ∆, trong mỗi trường hợp sau:

a) (P) nằm hoàn toàn phía trên trục hoành;

b) (P) nằm hoàn toàn phía dưới trục hoành;

c) (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành;

d) (P) tiếp xúc với trục hoành và nằm phía trên trục hoành.

Lời giải

a) Do (P) nằm hoàn toàn phía trên trục hoành nên

- Bề lõm của đồ thị phải quay lên trên, do đó hệ số a > 0.

- Giá trị của hàm số y > 0 nên −Δ4a > 0 (vì −Δ4a là tung độ của đỉnh), mà a > 0 nên 4a > 0, do đó - ∆ > 0 ⇔ ∆ < 0.

b) Vì (P) nằm hoàn toàn phía dưới trục hoành nên:

- Bề lõm của đồ thị phải quay xuống dưới, do đó hệ số a < 0.

- Giá trị của hàm số y < 0 nên biệt thức −Δ4a < 0 (vì −Δ4a là tung độ của đỉnh), mà a < 0 nên 4a < 0, do đó - ∆ > 0 ⇔ ∆ < 0.

c) Do (P) cắt trục hoành tại hai điểm phân biệt nên phương trình ax2 + bx + c = 0 có hai nghiệm phân biệt, vậy biệt thức ∆ > 0.

Lại có (P) có đỉnh nằm phía dưới trục hoành và cắt trục hoành tại 2 điểm phân biệt nên bề lõm của đồ thị phải quay lên trên nên hệ số a > 0.

d) Do (P) tiếp xúc với trục hoành nên phương trình ax2 + bx + c = 0 có nghiệm kép, vậy biệt thức ∆ = 0.

Lại có (P) nằm phía trên trục hoành nên bề lõm của đồ thị phải quay lên trên nên hệ số a > 0.

Bài 6.12 trang 16 Toán 10 Tập 2: Hai bạn An và Bình trao đổi với nhau.

An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8 m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5 m là 2,93 m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12 m.

Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.

Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

Lời giải

Cổng Trường Đại học Bách khoa Hà Nội có dạng là một parabol, gọi dạng parabol này là y = ax2 + bx + c với a ≠ 0.

Chọn hệ trục tọa độ Oxy như hình vẽ với Oy là trục đối xứng của cổng:

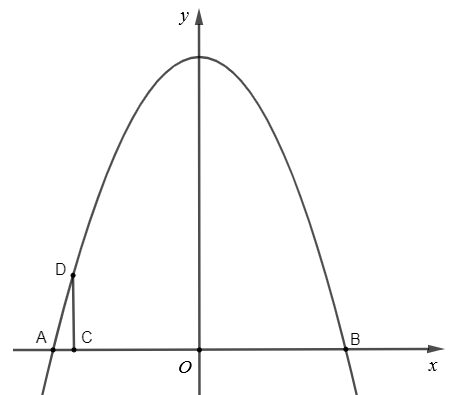
Khoảng cách giữa hai chân cổng AB = 8 m.

Vì Oy là trục đối xứng của parabol nên O là trung điểm của AB, do đó AO = OB = 4 m.

Lấy điểm C cách A một khoảng 0,5 m, theo bài ra, chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5 m là 2,93 m nên CD = 2,93 m.

CO = AO - AC = 4 - 0,5 = 3,5 m.

Vậy ta xác định được tọa độ các điểm: A(- 4; 0), B(4; 0), C(- 3,5; 0), D(- 3,5; 2,93).

Parabol đi qua các điểm A, B, D nên phương trình y = ax2 + bx + c thỏa mãn tọa độ các điểm A, B, D, thay tọa độ các điểm tương ứng ta có:

0 = a . (- 4)2 + b . (- 4) + c ⇔ 16a - 4b + c = 0 (1)

0 = a . 42 + b . 4 + c ⇔ 16a + 4b + c = 0 (2)

2,93 = a . (- 3,5)2 + b . (- 3,5) + c = 0 ⇔ 12,25a - 3,5b + c = 2,93 (3)

Lấy (2) trừ (1) theo vế ta được 8b = 0 ⇔ b = 0 thay vào (1) và (3) ta có hệ:

16a+c=012,25a+c=2,93⇔a=−293375c=4688375

Vậy parabol y=−293375x2+4688375 có tọa độ đỉnh I0; 4688375.

Chiều cao của cổng parabol là tung độ đỉnh I và bằng 4688375≈12,5m.

Vậy kết quả của bạn An tính ra là không chính xác.

Bài 6.13 trang 16 Toán 10 Tập 2: Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau.

a) Tính diện tích mảnh vườn hình chữ nhật được rào theo chiều rộng x (mét) của nó.

b) Tính kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác Hùng có thể rào được.

Lời giải

a) Bác Hùng dùng lưới để rào thành một mảnh vườn hình chữ nhật có chiều rộng x (mét).

Do tấm lưới dài 40 m nên chu vi của mảnh vườn hình chữ nhật là 40 m.

Nửa chu vi của mảnh vườn là 40 : 2 = 20 m.

Chiều dài của mảnh vườn rào là: 20 - x (m).

Diện tích mảnh vườn hình chữ nhật là: S(x) = x . (20 - x) = - x2 + 20x (m2).

Như vậy, diện tích S(x) của mảnh vườn là hàm số của chiều rộng x.

b) Để tìm diện tích lớn nhất của mảnh vườn hình chữ nhật bác Hùng có thể rào được, ta tính giá trị lớn nhất của hàm số S(x).

Hàm số S(x) là hàm số bậc hai với a = - 1, b = 20, c = 0.

Tọa độ đỉnh của đồ thị hàm số S(x) = - x2 + 20x là I(10; 100).

Vậy hàm số S(x) đạt giá trị lớn nhất là S =100 tại x = 10.

Khi đó chiều dài là 20 - 10 = 10 (m).

Vậy để mảnh vườn rào được có diện tích lớn nhất thì bác Hùng nên rào lưới thép gai thành hình vuông có độ dài cạnh là 10 m hay kích thước của mảnh vườn là 10 m × 10 m.

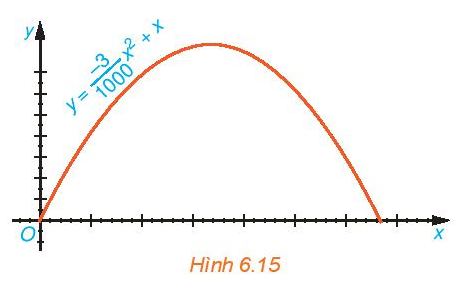
Bài 6.14 trang 16 Toán 10 Tập 2: Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình y=−31000x2+x, trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vậy so với mặt đất (H.6.15).

a) Tìm độ cao lớn nhất của vật trong quá trình bay.

b) Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.

Lời giải

a) Vật đạt độ cao lớn nhất khi y đạt giá trị lớn nhất.

Do đó, độ cao lớn nhất của vật trong quá trình bay chính là tung độ đỉnh của parabol có phương trình y=−31000x2+x.

Hoành độ đỉnh là x=−b2a=−12.−31000=5003.

Tung độ của đỉnh là y5003=−31000.50032+5003=2503.

Vậy độ cao lớn nhất trong quá trình bay của vật là 2503 m.

b) Vật chạm đất tức là y = 0, hay −31000x2+x=0⇔x−31000x+1=0⇔x=0x=10003.

Loại trường hợp x = 0 do đây là vị trí điểm gốc tọa độ O.

Vậy tầm xa của quỹ đạo là 10003 m.

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Giải Toán 10 trang 11 Tập 2

Giải Toán 10 trang 12 Tập 2

Giải Toán 10 trang 13 Tập 2

Giải Toán 10 trang 15 Tập 2

Giải Toán 10 trang 16 Tập 2

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 6

Bài 19: Phương trình đường thẳng

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.